Your first day as an estate agent

The data lives, among many other famous datasets, in the mlbench package.

data(BostonHousing)

In this post, I want to go over some general guidelines to consider when building a machine learning workflow. But if you’re an estate agent, this is gold and can be used to build a pricing model for other houses in the area.

glimpse(BostonHousing)
## Rows: 506
## Columns: 14
## $ crim    <dbl> 0.00632, 0.02731, 0.02729, 0.03237, 0.06905, 0.02985, 0.08829…
## $ zn      <dbl> 18.0, 0.0, 0.0, 0.0, 0.0, 0.0, 12.5, 12.5, 12.5, 12.5, 12.5, …
## $ indus   <dbl> 2.31, 7.07, 7.07, 2.18, 2.18, 2.18, 7.87, 7.87, 7.87, 7.87, 7…
## $ chas    <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ nox     <dbl> 0.538, 0.469, 0.469, 0.458, 0.458, 0.458, 0.524, 0.524, 0.524…
## $ rm      <dbl> 6.575, 6.421, 7.185, 6.998, 7.147, 6.430, 6.012, 6.172, 5.631…
## $ age     <dbl> 65.2, 78.9, 61.1, 45.8, 54.2, 58.7, 66.6, 96.1, 100.0, 85.9, …
## $ dis     <dbl> 4.0900, 4.9671, 4.9671, 6.0622, 6.0622, 6.0622, 5.5605, 5.950…
## $ rad     <dbl> 1, 2, 2, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 4…
## $ tax     <dbl> 296, 242, 242, 222, 222, 222, 311, 311, 311, 311, 311, 311, 3…
## $ ptratio <dbl> 15.3, 17.8, 17.8, 18.7, 18.7, 18.7, 15.2, 15.2, 15.2, 15.2, 1…
## $ b       <dbl> 396.90, 396.90, 392.83, 394.63, 396.90, 394.12, 395.60, 396.9…
## $ lstat   <dbl> 4.98, 9.14, 4.03, 2.94, 5.33, 5.21, 12.43, 19.15, 29.93, 17.1…
## $ medv    <dbl> 24.0, 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 1…

• crim per capita crime rate by town
• zn proportion of residential land zoned for lots over 25,000 sq. ft
• indus proportion of non-retail business acres per town
• chas Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
• nox nitric oxide concentration (parts per 10 million)
• rm average number of rooms per dwelling
• age proportion of owner-occupied units built prior to 1940
• dis weighted distances to five Boston employment centers
• rad index of accessibility to radial highways
• tax full-value property tax rate per $10,000
• ptratio pupil-teacher ratio by town
• b proxi for proportion of African American by town
• lstat percentage of lower status of the population
• medv median value of owner-occupied homes in $1000s

The prices of the house indicated by the variable medv is the target variable, and the remaining are the feature variables based on which we will predict the value of a house.

Let’s plant seed for reproducibility.

set.seed(42)

It’s important to split the dataset into training and testing data. The data can be split using initial_split. I’ll use 80% for training, fit the model and tune its parameters, and set aside 20% for testing, when we will evaluate the model’s performance.

boston_split <- BostonHousing %>% 
  initial_split(prop = .8)

We need to pull them both.

train_tbl <- training(boston_split)
test_tbl <- testing(boston_split)

And we will want to cross-validate. vfold_cv helps to create a cross-validated version of the training set. Default is 10 partitions, which is great.

folds <- vfold_cv(train_tbl)

The three questions

No matter what you’re dealing with, in real life most datasets aren’t provided ready to use. While working with mlbench you shouldn’t need to be prepared for the worst, but numeric aren’t neatly scaled or centered in their natural state and some might even be correlated.

rec_obj <- train_tbl %>% 
  recipe(medv ~ .) %>%
  step_center(all_numeric(), -all_outcomes()) %>%
  step_scale(all_numeric(), -all_outcomes()) %>%
  step_corr(all_numeric(), -all_outcomes()) %>% 
  prep(data = train_tbl)

We certainly want to review what will happen to the data.

rec_obj
## Data Recipe
## 
## Inputs:
## 
##       role #variables
##    outcome          1
##  predictor         13
## 
## Training data contained 405 data points and no missing data.
## 
## Operations:
## 
## Centering for crim, zn, indus, nox, rm, age, dis, rad, ... [trained]
## Scaling for crim, zn, indus, nox, rm, age, dis, rad, ... [trained]
## Correlation filter removed tax [trained]

Turns out tax is above the default (.9) and will get discarded, whereas all other predictors will be directed to scaling and centering. juice can reveal this by extracting the pre-processed data.

rec_obj %>%
  prep(train_tbl) %>%
  juice()
## # A tibble: 405 x 13
##      crim      zn  indus chas     nox     rm     age    dis    rad ptratio     b
##     <dbl>   <dbl>  <dbl> <fct>  <dbl>  <dbl>   <dbl>  <dbl>  <dbl>   <dbl> <dbl>
##  1 -0.408  0.249  -1.25  0     -0.105  0.392 -0.0623 0.0998 -0.963  -1.44  0.432
##  2 -0.406 -0.514  -0.547 0     -0.702  0.171  0.420  0.517  -0.846  -0.269 0.432
##  3 -0.406 -0.514  -1.26  0     -0.797  0.184 -0.291  1.04   -0.729   0.153 0.402
##  4 -0.399  0.0157 -0.430 0     -0.226 -0.415 -0.0130 0.800  -0.495  -1.49  0.418
##  5 -0.392  0.0157 -0.430 0     -0.226 -0.186  1.03   0.986  -0.495  -1.49  0.432
##  6 -0.384  0.0157 -0.430 0     -0.226 -0.960  1.16   1.05   -0.495  -1.49  0.321
##  7 -0.389  0.0157 -0.430 0     -0.226 -0.426  0.666  1.29   -0.495  -1.49  0.322
##  8 -0.382  0.0157 -0.430 0     -0.226  0.108  0.962  1.17   -0.495  -1.49  0.384
##  9 -0.395  0.0157 -0.430 0     -0.226 -0.419  0.561  1.12   -0.495  -1.49  0.432
## 10 -0.398  0.0157 -0.430 0     -0.226 -0.591 -0.984  0.748  -0.495  -1.49  0.363
## # … with 395 more rows, and 2 more variables: lstat <dbl>, medv <dbl>

Progressing through an analysis, you’ll no doubt have to choose a model. parsnip tries to remove the hurdles by providing similar interfaces to different models. If you go for a random forest and would like to adjust the number of trees there are different argument names to remember:

• randomForest::randomForest uses ntree,
• ranger::ranger uses num.trees,
• Spark’s sparklyr::ml_random_forest uses num_trees.

Which most conveniently becomes trees with parsnip. Here we are going to set the engine (set_engine) to ranger and tune mtry as well within set_args.

rf_model <- rand_forest() %>%
  set_args(mtry = tune(), trees = tune()) %>%
  set_engine("ranger", importance = "impurity") %>%
  set_mode("regression") 

Establishing a workflow that encompasses the main stages of the process is a great way to ensure you keep on track and provide that extra healthy safety layer.

rf_workflow <- workflow() %>%
  add_recipe(rec_obj) %>%
  add_model(rf_model)

Finally, there’s one last important step before fitting the model: tuning. Let’s specify in a grid the values we want to try for mtry and trees.

rf_grid <- expand.grid(mtry  = 1:10, 
                       trees = c(250, 500, 750))

Time for the CPU do its magic. It will use the recipe and model we’ve been working on and tune_grid will compute a set of performance metrics (rmse and rsq) across 10 resamples of the data.

rf_tune <- rf_workflow %>%
  tune_grid(resamples = folds,
            grid      = rf_grid,
            metrics   = metric_set(rmse, rsq))

For the most curious mind collect_metrics extracts and formats the produced results. We can pipe this into a plot.

rf_tune %>% 
  collect_metrics() %>% 
  filter(.metric == "rmse") %>% 
  mutate_at("trees", as.factor) %>% 
  ggplot(aes(mtry, mean, color = trees)) +
  geom_point(alpha = .7) +
  geom_line() +
  theme_ipsum() +
  scale_color_ipsum() +
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank()) +
  scale_x_continuous(n.breaks = 10)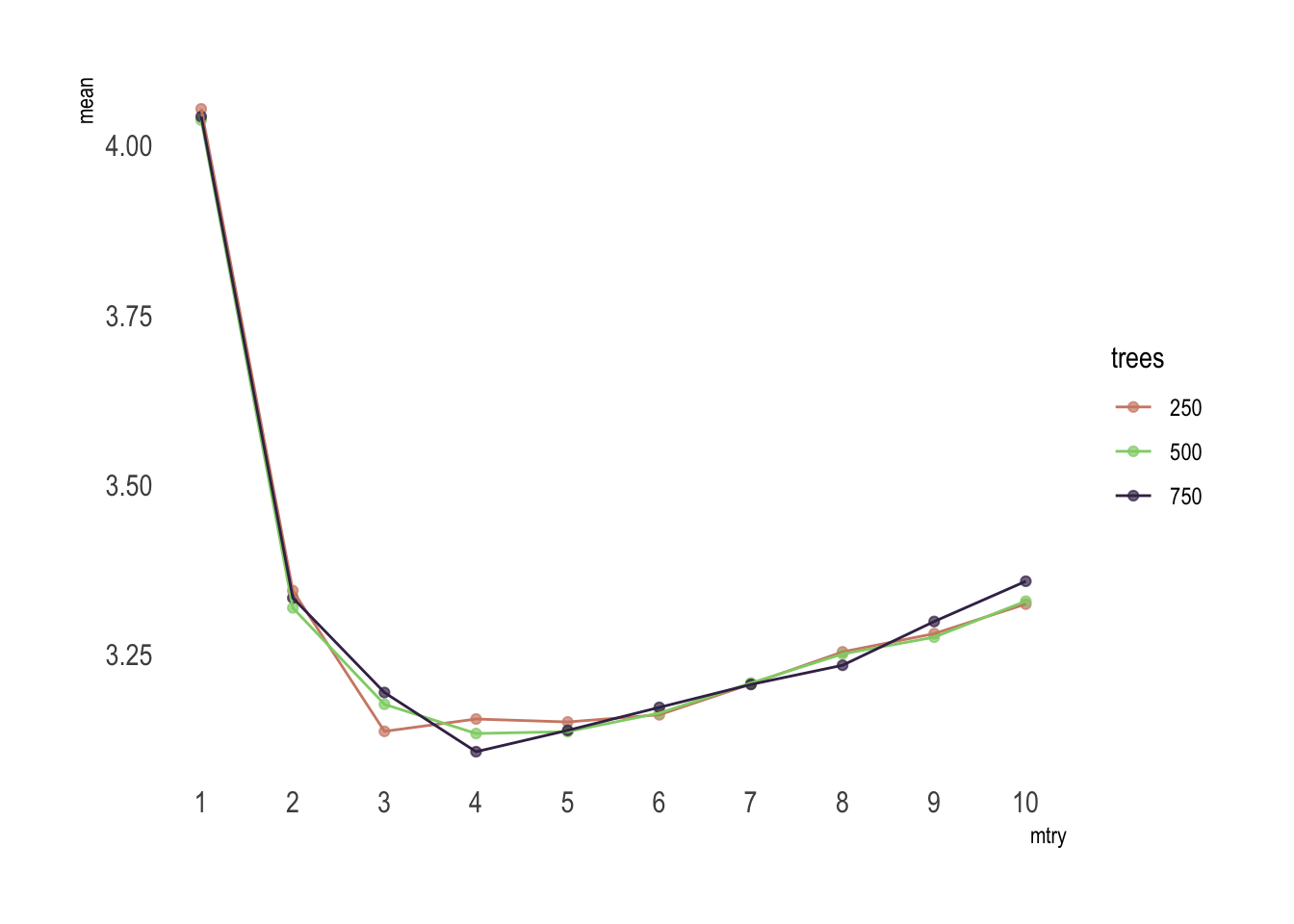

Or if you feel a bit lazy, you can use select_best() to find the tuning parameter combination with the best performance values.

rf_param <- rf_tune %>%
  select_best(metric = "rmse")

Build it on

How you answer all of these questions depends on your data, model, and the difficulty of the task, but now we’re ready to actually fit the final model. After determining the best parameters, finalize_workflow comes in handy to plug these parameters into the workflow.

rf_workflow <- rf_workflow %>%
  finalize_workflow(rf_param)

Finally, this complete workflow is injected with the full dataset via last_fit.

rf_fit <- rf_workflow %>%
  last_fit(boston_split)

This is absolutely right. Since we supplied the split object when we fitted the workflow, metrics will be evaluated on the test set only. Metrics and predictions are now close at hand.

rf_fit %>% 
  collect_metrics()
## # A tibble: 2 x 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       4.90 
## 2 rsq     standard       0.792

rf_fit %>% 
  collect_predictions()
## # A tibble: 101 x 4
##    id               .pred  .row  medv
##    <chr>            <dbl> <int> <dbl>
##  1 train/test split  36.0     3  34.7
##  2 train/test split  36.0     4  33.4
##  3 train/test split  33.4     5  36.2
##  4 train/test split  21.0    16  19.9
##  5 train/test split  19.9    20  18.2
##  6 train/test split  15.4    24  14.5
##  7 train/test split  15.6    33  13.2
##  8 train/test split  14.7    35  13.5
##  9 train/test split  29.0    40  30.8
## 10 train/test split  18.1    49  14.4
## # … with 91 more rows

These are obviously predictions made on the test set only as there are 101 rows total. The performance is very good, with a RMSE of 4.9 and Rsq of 0.79.

We can pipe this into ggplot2 to visualize the residuals.

rf_fit %>% 
  collect_predictions() %>% 
  ggplot(aes(medv, medv - .pred)) +
  geom_point(alpha = .7) +
  theme_ipsum() +
  geom_abline(intercept = 0, slope = 0, linetype = "dashed") +
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank())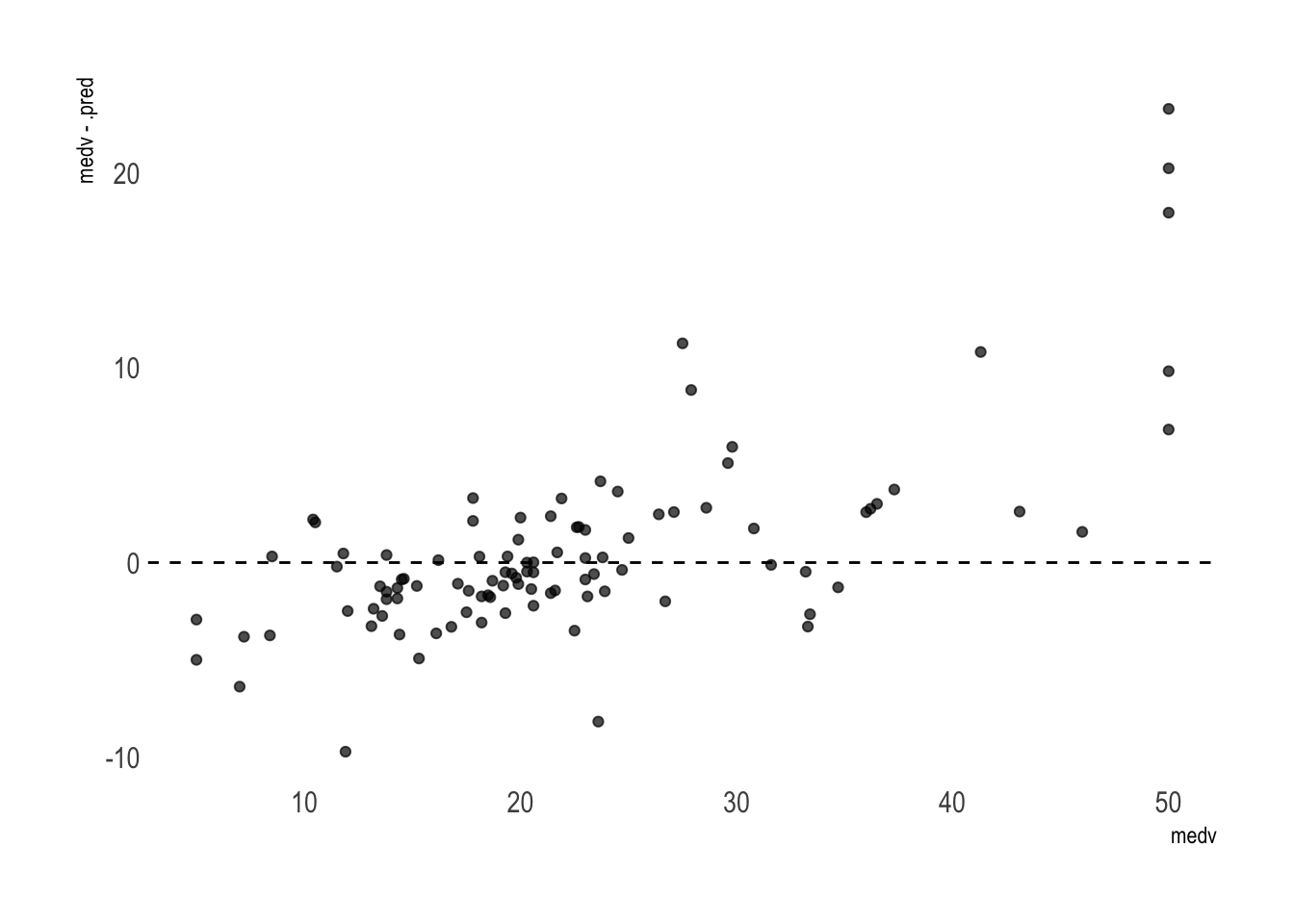

Overall it’s good. But the model tends to somehow overprice the cheapest houses and clearly underprice the most luxurious properties. It would certainly help to collect more data on the lower and higher ends to further improve the result. Alternatively, we could filter out the most extreme cases to get a better estimation of how far off we are on average for the most common houses.

Wrap it up

Okay, once we’ve evaluated the model and are happy with predictions we definitively want to train it again, this time on the full dataset, to then use it and predict the values for new data. Well, we will fit, simply.

rf_fin <- rf_workflow %>% 
  fit(BostonHousing)

Being able to explain the model to, let’s say the management team from bostonrealestate.com or the field agents, is primordial. Various elements from a workflow object can be extracted via workflow_extractors. Here we pull the fit.

rf_obj <- pull_workflow_fit(rf_fin)$fit

And since a picture is worth a thousand words we can present the variable importance.

tibble(var = rf_obj$variable.importance,
       nam = rf_obj$variable.importance %>% names(),
       ) %>% 
  ggplot(aes(var, reorder(nam, var))) +
  geom_bar(stat  = 'identity', 
           alpha = .7, 
           width = .8
           ) +
  theme_ipsum() +
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        axis.text.x = element_blank()
        )

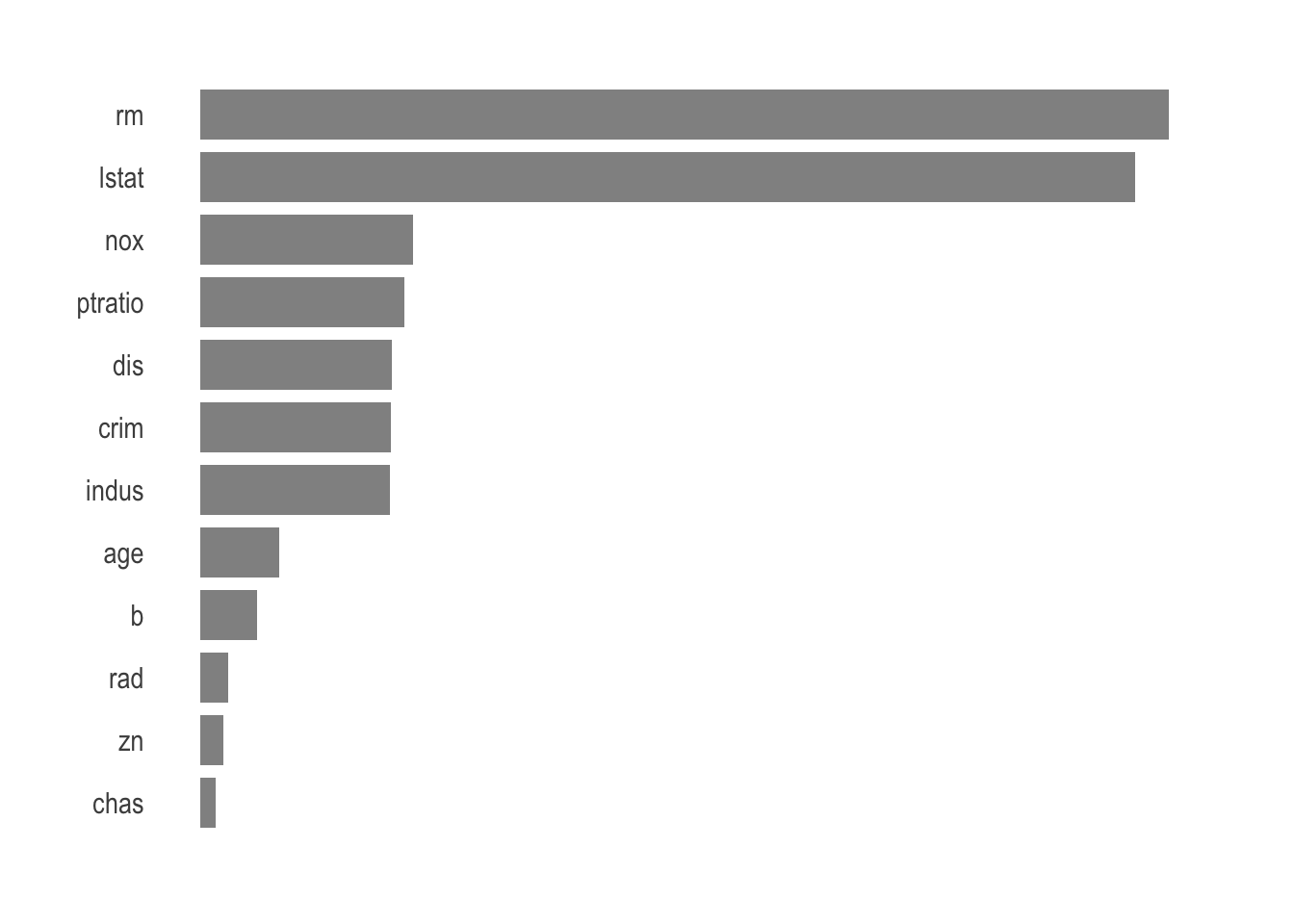
The average number of rooms per dwelling and percentage of lower status of the population are the most important variables when it comes to predicting the price of a house in Boston.

Awesome, now you can simply go ahead with this random forest or set another engine within your workflow. It’s really up to you and so easy to change your mind. That’s really the most amazing part of a tidy workflow.